Аппроксимация данных

Напомним, что регрессионный анализ это вид статистического анализа, используемый для прогнозирования. Регрессионный анализ позволяет оценить степень связи между переменными, предлагая механизм вычисления предполагаемого значения переменной из нескольких уже известных значений.
Линиями тренда можно дополнить ряды данных, представленные на ненормированных плоских диаграммах с областями, линейчатых диаграммах, гистограммах, графиках, биржевых, точечных и пузырьковых диаграммах. Использование линии тренда того или иного вида определяется типом данных. Нельзя дополнить линиями тренда ряды данных на объемных диаграммах, нормированных диаграммах, лепестковых диаграммах, круговых и кольцевых диаграммах.
Более ясно закономерность в развитии данных показывает сглаженная кривая. Она строится по точкам скользящего среднего, где под скользящим средним подразумевается последовательность средних чисел, каждое из которых вычислено по некоторому подмножеству ряда данных.

Добавление линии тренда или скользящего среднего к рядам данных

В Excel используются шесть различных видов линий тренда (аппроксимация и сглаживание), которые могут быть добавлены в диаграмму (рис. 18.11): 1) Линейная аппроксимация (Linear) — это прямая линия, наилучшим образом описывающая набор данных. Уравнение прямой у=ах+Ь, где а — тангенс угла наклона, b — точка пересечения прямой с осью у. Линейная аппроксимация применяется для переменных, которые увеличиваются или убывают с постоянной скоростью.
2) Логарифмическая аппроксимация (Logarithmic) хорошо описывает положительные, так и отрицательные величины, которые вначале быстро растут или убывают, а затем постепенно стабилизируется. Логарифмическая аппроксимация использует уравнение у=с* lnx+Ь, где с и b константы, In — натуральный логарифм.
3) Полиномиальная аппроксимация (Polynomial) используется для описания величин, попеременно возрастающих и убывающих. Ее целесообразно применять для анализа большого набора данных нестабильной величины. Степень полинома определяется количеством экстремумов (максимумов и минимумов) кривой. Полином второй степени может описать только один максимум или минимум. Полином третьей степени имеет один или два экстремума. Полином четвертой степени может иметь не более трех экстремумов. Полиномиальная аппроксимация описывается уравнением y=a+ciXi+C2X2++Cigx18, где a, Cj—Cjg — константы. Требуемая степень полинома задается в поле Степень (рис.). Максимальная величина степени — 18.

4) Степенная аппроксимация (Power) дает хорошие результаты, если зависимость, которая содержится в данных, характеризуется постоянной скоростью роста. Примером такой зависимости может служить график ускорения автомобиля. Если в данных имеются нулевые или отрицательные значения, использование степенного приближения невозможно. Степенная аппроксимация описывается уравнением у=а * хn, где а и n — константы.
5) Экспоненциальную аппроксимацию (Exponential) следует использовать в том случае, если скорость изменения данных непрерывно возрастает. Однако для данных, которые содержат нулевые или отрицательные значения, этот вид приближения неприменим. Экспоненциальная аппроксимация описывается уравнением у= а • ebx, где а и b — константы.
6) Линейная фильтрация (Moving average) позволяет сгладить колебания данных и таким образом более наглядно показать характер зависимости. Такая линия тренда строится по определенному числу точек (она задается параметром Тонки (Period). Элементы данных усредняются, и полученный результат используется в качестве среднего значения для приближения. Так, если параметр Тонки равен 2, первая точка сглаживающей кривой определяется как среднее значение первых двух элементов данных, вторая точка — как среднее следующих двух элементов и так далее. Для расчета скользящего среднего используется уравнение у= (Aj+Aj_i++Aj_n+i)/n.

Добавление линии тренда к рядам данных

Для добавления линии тренда к рядам данных выполните следующие действия:

выделите ряд данных, к которому нужно добавить линию тренда или скользящее среднее;
выберите команду Добавить линию тренда (Add Trendline ) в меню Диаграмма (Chart). На вкладке Тип (Туре) выберите нужный тип регрессионной линии тренда или линии скользящего среднего (рис. 18.11);

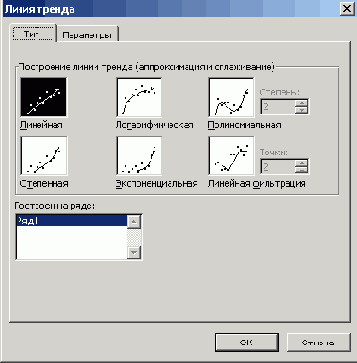
Рис. 18.11 Выбор линии тренда

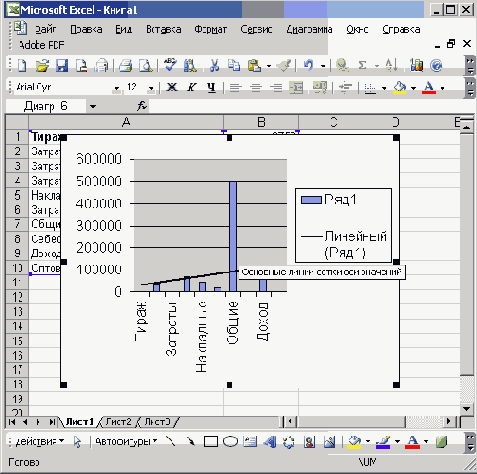
Рис. 18.12 Диаграмма с нанесенной линией тренда

при выборе типа Полиномиальная (Polynomial) введите в поле Степень (Order) наибольшую степень для независимой переменной;
при выборе типа Скользящее среднее (Moving Average) введите в поле Точки (Period) число точек, используемых для расчета скользящего среднего.

Все ряды данных диаграммы, поддерживающей линии тренда перечислены в поле Построен на ряде (Based On Series) . Для добавления линии тренда к другим рядам выберите нужное имя в поле, а затем выберите нужные параметры. Если вариант Скользящее среднее (Moving Average) выбран для точечной диаграммы, результат будет зависеть от порядка расположения значений X во входном диапазоне. Чтобы получить правильный результат, необходимо отсортировать значения X перед построением линии скользящего среднего.

Надежность линии тренда

Оценка надежности линии тренда к фактическим данным выполняется по показателю определенности или величине R в квадрате. R может изменяться от 0 до 1. Чем больше величина этого показателя, тем достовернее линия тренда. Значение R2 автоматически рассчитывается Excel при подборе линии тренда к данным. Это значение можно отобразить на диаграмме.
Для вывода значения R-квадрат для линии тренда щелкните эту линию, и выберите команду Выделенная линия тренда (Selected Trendline) в меню Формат (Format) . На вкладке Параметры (Options) установите флажок поместить на диаграмму величину достоверности аппроксимации (R*2) (Display R-squared value on chart) (рис. 18.13). Отметим, что для скользящего среднего значение R-квадрат не может быть отображено.

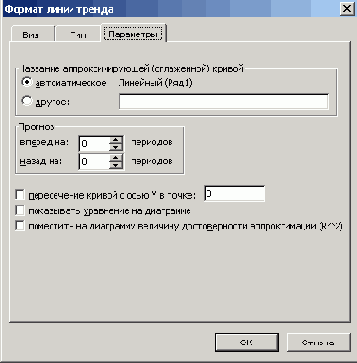
Рис. 18.13 вывод значения R-квадрат для линии тренда

Содержание раздела

Forekc.ru
Рефераты, дипломы, курсовые, выпускные и квалификационные работы, диссертации, учебники, учебные пособия, лекции, методические пособия и рекомендации, программы и курсы обучения, публикации из профильных изданий